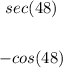Given the Trigonometric Functions:
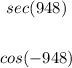
Using your calculator you get:
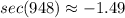
By definition, Secant is negative in Quadrant III.
Finds its Reference Angle as follows:
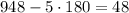
Because:
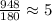
Then, you get:
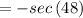
Notice that:
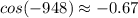
Then, you can conclude that it is in Quadrant II.
Therefore its Reference Angle is:
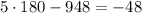
So you can set up:
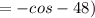
By definition:
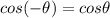
Therefore, you can rewrite it in this form:
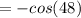
Hence, the answer is: