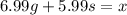Given data:
The coach of a soccer team is ordering trophies for the players.
They can choose between 2 types of trophies.
The cost of gold soccer trophies =$6.99.
The cost of silver trophies = $5.99.
let the g be the number of gold trophies and let s be the no. of silver trophies.
let the total amount that coach pays for all the trophies. be x.
The expression that represnts the total amount is