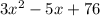Given the expression:
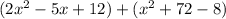
You have to combine the like terms together, that is group the terms together according to their variable and exponent index. The x-square terms have the same base number "x", and the same exponent "2", this means they are like terms.
The constants, or "alone numbers" are like terms too.
First, order them, I will use parentheses to separate the different groups
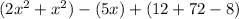
You have three groups of terms, those who contain "x²", those who contain "x" and the constants.
Now, you can combine them by solving the operations between them. For the constants, you have to add/subtract them.
For the x-square terms, you have to add/subtract their coefficients (i.e. the numbers that multiply "x²")
-5x is the only term of its group so you have to leave it as it is

After combining the like terms the simplified expression is