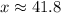As you can see in the picture given in the exercise, the trapezoid can be divided into two figures: a rectangle and a Right triangle.
Let be "b" the base of the triangle (the horizontal distance indicated in the exercise). You can set up that:
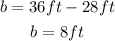
Now you can use the following Inverse trigonometric function to find the measure of the angle "x":
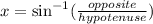
In this case:
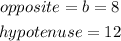
Then, substituting values and evaluating, you get:
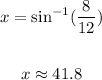
The answer is: