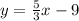We need to find the equation of the line that passes through the points (0,-9) and (6,1).
To solve it we're going to use the equation of a line given as:
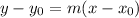
Where m represents the slope of the line and y0, x0 is any point of the line.
To find, firstly, the slope we're going to use the following formula:
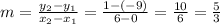
Now, we reply to the slope in the equation line and chose any point from the ones given by the statement. To make easily the counts we can use (0,-9).
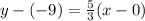
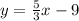
Then the correct answer for the equation of the line that passes through the points (0,-9) and (6,1) is: