Question

Point Tis on line segment SU. Given TU = 4x + 1, SU = 8, and ST = 3x,determine the numerical length of TU.

Answer 1

The point T is in the line SU, which means that it is between the points S and U. Therefore, the distance ST + TU must be equal to the distance between S and U. We know the distance between S and T and the distance between T and U, therefore:

`ST\text{ + TU = SU}`

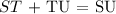
Applying the data provided by the problem:

`\begin{gathered} 3x\text{ + (4x + 1) = 8} \\ 3x\text{ + 4x + 1 = 8} \\ 7x\text{ = 8 -1} \\ 7x\text{ = 7} \\ x\text{ = }(7)/(7)\text{ = 1} \end{gathered}`

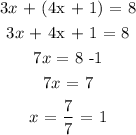
We now need to find the distance between T and U, which is given by the following expression:

`TU\text{ = 4x + 1}`

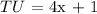
Applying the data from x we calculated:

`TU\text{ = 4}\cdot1\text{ + 1 = 4 + 1 = 5}`

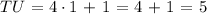
The numerical length of the line TU is 5.