Question

Write the equation in siope-intercept form for the line that passes through the given pointand is perpendicular to the given equation2x+10y = 20 and passes through (2, 3)

Answer 1

For a line in the form:

`\begin{gathered} ax+by=c \\ The\text{ slope m is:} \\ m=-(a)/(b) \end{gathered}`

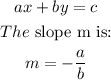
In this case, for the line 2x + 10y = 20 with a=2 and b=10 the slope is:

`\begin{gathered} m_1=-(a)/(b)=-(2)/(10) \\ m_1=-(1)/(5) \end{gathered}`

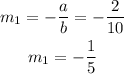
Now, two lines are perpendiculars if the slopes satisfy the following equation:

`m_2=-(1)/(m_1)`

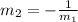
So, for the line we want the slope is:

`\begin{gathered} m_1=-(1)/(5) \\ m_2=-(1)/(m_1)=-(1)/((-(1)/(5)))=5 \end{gathered}`

Finally, the line pass througth the point (2, 3) with slope m=5, so the equation is:

`\begin{gathered} P_1=(2,3),m=5 \\ y=mx+b \\ \text{The P1 must satisfy the equation:} \\ 3=5\cdot2+b \\ b=3-10 \\ b=-7 \end{gathered}`

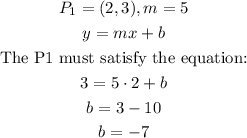
The equation of the line is y = 5x - 7