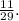To solve this problem we will use the following formula to compute the theoretical probability that an event occurs:
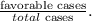
e) From the given table we get that there are 12 male students in Green club.
Since there are 100 students in total, we get that the theoretical probability of choosing a male student that is in Green club is:
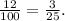
f) To answer this question we will use the following formula:
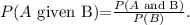
From the given table we get that there are 22 female students in Huskies with Heart, and there are a total of 58 female students, therefore:
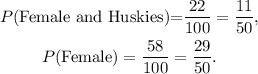
Therefore:
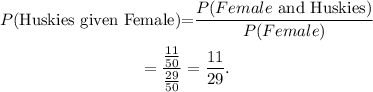
Answer:
e)
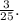
f)