Question

The base of an isosceles triangle has a length of 36 and a vertex anglemeasures 66 degrees. What is the length of each leg? Round to the nearest onehundredth of a foot.

Answer 1

The length of each leg of the isosceles triangle is obtained as follows:

Step 1: we make a sketch of the isosceles triangle and label it as below;

Step 2: we find the value of the base angle of the triangle as follows:

`\begin{gathered} S\text{ince the sum of angles in a triangle is 180 degrees, we have:} \\ x+x+66=180 \\ 2x+66=180 \\ 2x=180-66 \\ 2x=114 \\ x=(114)/(2) \\ x=57^o \end{gathered}`

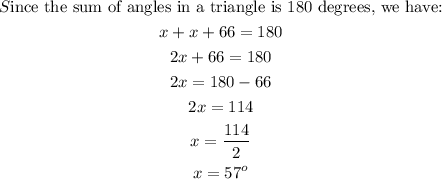
Thus the value of the angles at the base of the triangle is 57 degrees each.

Step 3: we update the sketch of the triangle with the new information

Step 4: we apply the sine rule to the triangle in order to obtain the length of each of the leg, a