Question

please see image61) After you pick up a spare, your bowling ball rolls without slipping back toward the ball rack with a linear speed of vi=2.62m/s. To reach the rack, the ball rolls up a ramp that rises through a vertical height of h=0.47m. (a) What is the linear speed of the ball when it reaches the top of the ramp? (b) If the radius of the ball were increased, would the speed found in part (a) increase, decrease, or stay the same? Explain.

Answer 1

(a) 0.53 m/s

(b) Stay the same

Step-by-step explanation

We know that the initial linear speed of the ball is vi = 2.62 m/s and that the height of the ramp is h = 0.47m

(a) To find the linear speed of the ball when it reaches the top of the ramp, we have to apply the principle of conservation of energy,

`KE_i+PE_i=KE_f+PE_f`

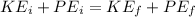
The initial potential energy of the ball is 0. Because the ball is rolling, the kinetic energy it has is the sum of the linear kinetic energy and the rotational kinetic energy,

`KE=(1)/(2)mv^2+(1)/(2)I(v^2)/(r^2)`

Where I is the moment of inertia of the ball - which is spherical,

`I=(2)/(5)mr^2`

Assuming that the ball is solid.

Thus, the principle of conservation of energy equation is,

`(1)/(2)mv^2_i+(1)/(2)\cdot(2)/(5)mr^2\cdot(v^2_i)/(r^2)+0=(1)/(2)mv^2_f+(1)/(2)\cdot(2)/(5)mr^2\cdot(v^2_f)/(r^2)+mgh`

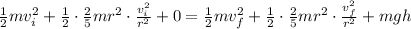
We can simplify the radius,

`(1)/(2)mv^2_i+(1)/(5)m^{}\cdot v^2_i^{}=(1)/(2)mv^2_f+(1)/(5)m^{}\cdot v^2_f^{}+mgh`

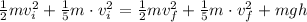
Add the two terms that have m and v, on each side of the equation,

`((1)/(2)+(1)/(5))mv^2_i=((1)/(2)+(1)/(5))mv^2_f+mgh`
`(7)/(10)mv^2_i=(7)/(10)mv^2_f+mgh`

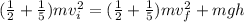
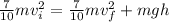
Now, note that m is a common factor, so it gets cancelled out,

`(7)/(10)mv^2_i=m((7)/(10)v^2_f+gh)`
`(7)/(10)v^2_i=(7)/(10)v^2_f+gh`

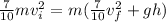
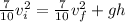
Remember that we want to find vf. The next step is to subtract gh from both sides of the equation,

`\begin{gathered} (7)/(10)v^2_i-gh=(7)/(10)v^2_f+gh-gh \\ (7)/(10)v^2_i-gh=(7)/(10)v^2_f \end{gathered}`

Then we have to multiply both sides by 10/7,

`\begin{gathered} (7)/(10)\cdot(10)/(7)v^2_i-(10)/(7)gh=(7)/(10)\cdot(10)/(7)v^2_f \\ v^2_i-(10)/(7)gh=v^2_f \end{gathered}`

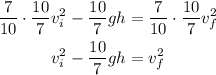
And finally, take the square root,

`v_f=\sqrt{v^2_i-(10)/(7)gh}`

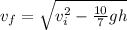
Now we just have to replace vi = 2.62m/s, g = 9.81m/s² and h = 0.47m,

`v_f=\sqrt[]{(2.62m/s)^2-(10)/(7)9.81m/s^2\cdot0.47m}`
`v_f=\sqrt[]{6.8644m^2/s^2-6.5867m^2/s^2}`
`v_f=\sqrt[]{0.2777m^2/s^2}\approx0.53m/s`

The linear velocity of the ball when it reaches the top of the ramp is 0.53m/s, rounded to the nearest hundredth.

(b) If the radius of the ball were increased, the speed found in part (a) would stay the same. Note that the expression we got from the principle of conservation of energy for the final linear speed depends neither on the radius nor on the mass of the ball.