The surface area of a hemisphere is given as 12.5 square feet. It is required to find the volume of the hemisphere.
To do this, equate the given surface area to the formula, find the radius, and then substitute the radius into the volume formula to find the volume.
The surface area of a hemisphere radius, r is given as:
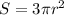
Substitute S=12.5 into the formula and solve for r in the resulting equation:
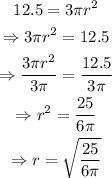
The volume of a hemisphere is given as:
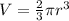
Substitute the calculated value of r into the volume formula:
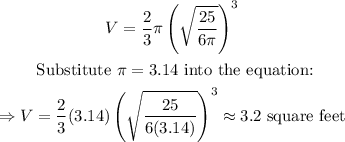
The required volume is about 3.2 square feet.