Given that
The equation of a parabola is y = (x-3)²-8
and we have to find its vertex.
Explanation -
First, we will write the given equation in the form of y = ax² +bx+c---------(i)
Then, we will use the formula

y = (x-3)²-8
y = x² + 9 - 6x - 8
y = x² - 6x + 1-------------(ii)
Comparing equation (i) and (ii) we have
a = 1, b = -6 and c = 1
and from this equation we can find the vertex and the formula for vertex is
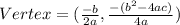
On substituting the values we have
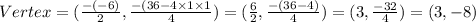
The coordinates of the vertex is (3,-8)
Hence, the final answer is (3,-8)