Given the function:
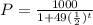
Where:
• P is the size of the population of toads
,
• t is the number of years after it is intriduced in a wetlands.
Let's find how long it will take the population to reach 750 toads.
To find the time, substitute 750 for P and solve for t.
We have:
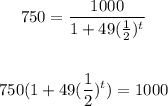
• Divide both sides by 750:
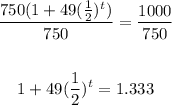
• Subtract 1 from both sides:
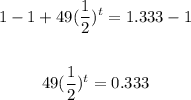
• Divide both sides by 49:
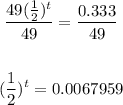
• Solving further, we have:
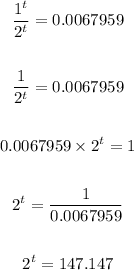
• Take the natural loagrithm of both sides:
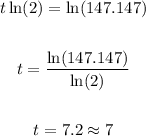
Therefore, it will take the toad population approximately 7 years to reach 750 toads.
ANSWER:
7 years