Question

Trent and Dyson pull opposite side of a shopping cart that has a mass of 13kg. Trent pulls the cart to the right with a force of 85N, and Dyson pulls the cart to the left with a force of 96N. Assume there is no friction. A. Draw the free-body diagram of the shopping cart. (Does not have to be perfect a box with arrows will be perfect)B. What is the normal force acting on the shopping cart?C. What is the acceleration of the shopping cart, include direction. D. If there were a coefficient of kinetic friction of .06 between the shopping cart and the ground, what would be the acceleration of the shopping cart?

Answer 1

ANSWER and EXPLANATION

A) Let us make a free body diagram of the shopping cart:

N represents the normal force acting on the cart

W represents the weight of the cart.

B) The normal force acting on the cart has the same magnitude as the weight but acts in the opposite direction.

Hence, the normal force on the cart is:

`N=|-mg|`

where g = acceleration due to gravity

m = mass of the cart

Therefore, the normal force is:

`\begin{gathered} N=|-13\cdot9.8| \\ N=127.4N \end{gathered}`

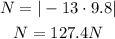
C) The net force acting on the body will cause the cart to accelerate in a particular direction (according to the second law of motion):

`F=ma`

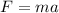
where a = acceleration

Taking the right as the positive direction and the left as the negative direction, means that the net force acting on the body is:

`\begin{gathered} +85+(-96)=ma \\ 85-96=ma \end{gathered}`

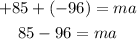
Input the value of m and solve for a:

`\begin{gathered} -11=13\cdot a \\ \Rightarrow a=-(11)/(13) \\ a=-0.85\text{ m/s}^(2) \end{gathered}`

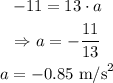
That is the acceleration of the shopping cart.

As we can see, the acceleration is in the left direction.

D) Now, we assume there is kinetic friction acting on the cart. The friction force must act in the opposite direction as the acceleration of the cart. This means that the friction acts in the right direction.

The net force acting on the body causes it to accelerate, which means that:

`85-96+F_f=ma`

where Ff = friction force

The friction force can be obtained by applying the formula:

`F_f=\mu N`

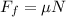
where μ = coefficient of friction; N = normal force.

The friction force is:

`\begin{gathered} F_f=0.06\cdot127.4 \\ F_f=7.64N \end{gathered}`

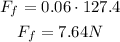
Therefore, the equation above becomes:

`85-96+7.64=ma`

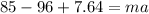
Input the value of m and solve for a:

`\begin{gathered} -3.36=13\cdot a \\ \Rightarrow a=(-3.36)/(13) \\ a=-0.26\text{ m/s}^(2) \end{gathered}`

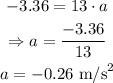
That is the acceleration of the shopping cart and as we can see, it still acts in the left direction.