How does this 4x^2-x-9 go to this (1 + √(145) )/(8)

Question

How does this 4x^2-x-9 go to this
`(1 + √(145) )/(8)`

Answer 1

Consider the given equation as,

`f(x)=4x^3+7x^2-11x-18`

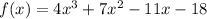
Equate the function to zero,

`4x^3+7x^2-11x-18=0`

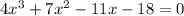
Since it is a cubic solution, we have to find the first zero using Hit and Trial Method,

`\begin{gathered} f(0)=4(0)^3+7(0)^2-11(0)-18=0+0-0-18 \\ f(-2)=4(-2)^3+7(-2)^2-11(-2)-18=0 \end{gathered}`

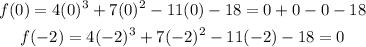
It is found that x=-2 is a zero of the cubic equation, it implies that(x+2) must be a factor of the polynomial.

So we can use the Long Division to find the other two zeroes as follows.

Thus, by the long division we obtained that,

`4x^3+7x^2-11x-18=(4x^2-x-9)(x+2)`

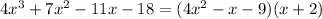
Equating the terms to zero,

`\begin{gathered} (4x^2-x-9)(x+2)=0 \\ 4x^2-x-9=0\text{ or }x+2=0 \\ 4x^2-x-9=0\text{ or }x=-2 \end{gathered}`

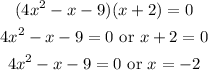
We already know the zero x= -2, the other two zeroes can be obtained from the other quadratic factor,

`\begin{gathered} 4x^2-x-9=0 \\ x=\frac{-(-1)\pm\sqrt[]{(-1)^2-4(4)(-9)}^{}}{2(4)} \\ x=\frac{1\pm\sqrt[]{1+144}^{}}{8} \\ x=\frac{1\pm12.0416^{}}{8} \\ x=\frac{1\pm12.0416^{}}{8}\text{ }or\text{ }x=\frac{1\pm12.0416^{}}{8} \\ x=1.63\text{ }or\text{ }x=-1.38 \end{gathered}`

Thus, the remaining two zeroes are 1.63 and -1.38 approximately.

So it concludes that the given cubic polynomial has the zeroes as -1.38, 1.63, and -2.