The Area of a Square is the square of the measure of one side of the square.
Hence, given the expression for the area of a square, express the given area as the square of an expression to get the measure of one side.
The given expression is:
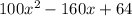
Rewrite the expression as:
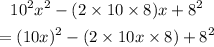
Recall the binomial expansion:
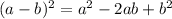
Substituting a=10x and b=8, it follows that the expression becomes:
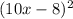
Since the area of a square is the square of the measure of one side, it follows that the measure of one side from the given expression is 10x-8.