Question

PreviousFind the sum of the arithmetic series 19 + 25 +31 +37 + where n=9.A. 774B. 396OC. 389D. 387Reset SelectionMaxt...

Answer 1

`D.\text{ }387`

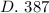
Step-by-step explanation

The sum of an arithmetic series is given by:

`S_n=(n)/(2)(2a+(n-1)d)`

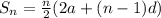
where a = first term

d = common difference

n = number of terms

From the question, we see that n is 9, the first term is 19, and the common difference is:

`\begin{gathered} d=25-19 \\ \\ d=6 \end{gathered}`

Therefore, the sum of the first 9 terms is:

`\begin{gathered} S_9=(9)/(2)(2(19)+(9-1)*6) \\ \\ S_9=(9)/(2)(38+48)=(9)/(2)*86 \\ \\ S_9=387 \end{gathered}`

The answer is option D.