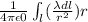Question

Write the expressions for the electric field strength due to several charges in terms of volume charge density, area charge density and linear charge density respectively

Answer 1

Step-by-step explanation:

5.6. 1: Electric Field of a Line Segment. Find the electric field a distance z above the midpoint of a straight line segment of length L that carries a uniform line charge density λ. dq=λdl.

Answer 2

Let's write the expressions for the electric field strength due to several charges in terms of the following:

• Volume charge density

,

• Area charge density

,

• Linear Charge density

The electric field strength can be said to be expression which shows the intensity of an electric field at a given location.

Now, we have the following expressions:

• Electric field strength due to several charges in terms of volume.

We have the expression:

`E_P=(1)/(4\pi\epsilon0)\int_V((\rho dV)/(r^2))r`

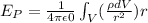
Where V is the volume, r is the distance between charges.

• Electric field strength in terms of area charge density:

We have the expression:

`E_p=(1)/(4\pi\epsilon0)\int_A((\sigma dA)/(r^2))r`

Where A is the area and r is the distance between the charges.

• Electric field strength in terms of linear charge density:

`E_P=(1)/(4\pi\epsilon0)\int_l((\lambda dl)/(r^2))r`

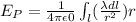
ANSWER:

• In terms of Volume charge density:

`(1)/(4\pi\epsilon0)\int_V((\rho dV)/(r^2))r`

• In terms of area charge density:

`(1)/(4\pi\epsilon0)\int_A((\sigma dA)/(r^2))r`

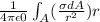
• In terms of linear charge density:

`(1)/(4\pi\epsilon0)\int_l((\lambda dl)/(r^2))r`