Question

If f(x) = 25 - x^2 and g(x) = x + 5 what is (f/g)(x)? write your answer in simplest form. When f(x) = 25 - x^2 and g(x) = x + 5, (f/g)(x)= __

Answer 1

Dividing functions

In order to divide a couple of functions, we simply divide their equations:

if f(x) = 25 - x²

and g(x) = x + 5

then

`\begin{gathered} (f)/(g)(x)=(f(x))/(g(x)) \\ \downarrow \\ (f)/(g)(x)=(25-x^2)/(x+5) \end{gathered}`

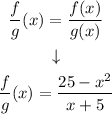
Simplifying the expression

In order to simplify the fraction we just factor the numerator:

25 - x² = (5 + x) (5 - x)

then

`(f)/(g)(x)=((5+x)(5-x))/(x+5)`

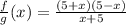
Since

5 + x = x + 5

we can cancel this factor from the denominator:

then,

`(f)/(g)(x)=5-x`

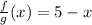
Answer: (f/g)(x) = 5 - x