Question

If a line contains the point (0, -1) and has a slope of 2, then which of the following points also lies on the line?

(2,1)
(0,1)
(1,1)

Answer 1

(1, 1) only.

Explanation:

Hey! Let's help you with your question here!

Let's begin by understanding what is given to us. We know that the line contains the point (0, -1) and has a slope of 2. What can we infer from this? We can create a slope-intercept equation of a line! How do we do that? Well, if you recall, the slope-intercept form is:

`y=mx+b`

We already have our slope of m, which is 2. Now we just need to find b. But how do we do that? Given that the line contains the point (0, -1), We can substitute the point into x and y and solve for b! It would look like this:

`-1=2(0)+b`

`-1=b`

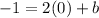
Now, that we've solved for b, we get the entire formula of:

`y=2x-1`

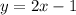
How do we know if the point is on the line or not? Well, for each point, we substitute the points (x and y) and see if they equal each other. If they don't, then they are not part of the line. If they do, they are considered part of the line. So it would be as such:

(2, 1):

`y=2x-1`

`1=2(2)-1`

`1=4-1`

`1\\eq 3`

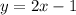
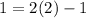
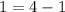
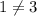
Since they don't equal each other, (2, 1) does not lie on the line.

(0, 1):

`y=2x-1`

`1=2(0)-1`

`1\\eq -1`

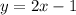
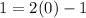
Since they don't equal each other, (0, 1) does not lie on the line.

(1, 1):

`y=2x-1`

`1=2(1)-1`

`1=2-1`

`1=1`

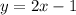
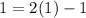
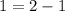
Turns out they do equal each other! Therefore, (1, 1) does lie on the line.

So out of all that we tested, the only point that also lies on the line is (1, 1).