The compound interest formula is given by
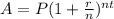
where A is the final amount including the principal P, r is the rate, n is the number or times interes and t is the time.
In our case, A= $43,278.39, P=$39,000, n=4 (for quarterly) and t is the unknown time.
We must find t in our formula. First, if we move P to the left hand side, we ger
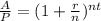
If we apply logarithm in both sides, we obtain
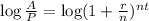
which gives,
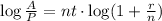
then, t is equal to
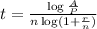
Therefore, by means of this formula, we can find t. If we substitute the given values into this formula ,we get
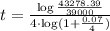
then, we have
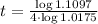
which is equal to
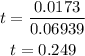
that is, by rounding up, the times is 0.3 years.