The given figure is a circular cylinder, and the pencil represents its diagonal.
We know that
• The pencil is 17 cm.
,
• The height is 15 cm.
Notice that the pencil, the height of the cup, and its width form a right rectangle.
We use Pythagorean's Theorem to find the width w. Remember that this theorem relates the square hypotenuse with the sum of the square of the legs.
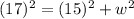
Let's solve for w
![\begin{gathered} 289-225=w^2 \\ w^2=64 \\ w=\sqrt[]{64} \\ w=8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9d5fawz1o4sfkegrzjqvgrns17b0k5a53k.png)
Therefore, the width is 8 centimeters long.