Question

Create a hand drawn sketch of the quadratic function: f(x)= x^2 -7x+3To earn full credit be sure to identify the vertex, the axis of symmetry and all intercepts. Include all work, calculations and steps needed (as described in this lesson) to create the graph.Let your teacher know if you have any questions on how to upload or share your written work.

Answer 1

Given the quadratic equation:

`y=x^2-7x+3`

To create a sketch of the quadratic function, follow the steps below.

Step 01: Find the x-intercepts.

The x-intercepts are the zeros of the function and can be found using the quadratic formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this question:

a = 1

b = -7

c = 3

Then,

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4\cdot1\cdot3}}{2\cdot1} \\ x=\frac{7\pm\sqrt[]{49-12}}{2}=\frac{7\pm\sqrt[]{37}}{2} \\ x_1=\frac{7-\sqrt[]{37}}{2}=0.5 \\ x_2=\frac{7+\sqrt[]{37}}{2}=6.5 \end{gathered}`

So, the equation has the points (0.5, 0) and (6.5, 0).

Step 02: Find the vertex.

The x-vertex is:

`\begin{gathered} x_v=(-b)/(2a) \\ x_v=(-(-7))/(2\cdot1) \\ x_v=(7)/(2) \\ x_v=3.5 \end{gathered}`

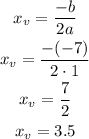
And, the y-vertex is:

`\begin{gathered} y_v=(-(b^2-4ac))/(4a) \\ y_v=(-\lbrack(-7)^2-4\cdot1\cdot3\rbrack)/(4\cdot1) \\ y_v=(-(49-12))/(4) \\ y_v=(-37)/(4)=-9.25 \end{gathered}`

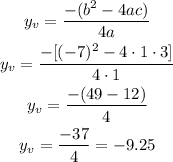
So, the vertex is the point (3.5, -9.25).

Step 03: Find the axis of symmetry.

The axis of symmetry is the line x = xv.

So, the axis of the symmetry is x = 3.5.

Step 04: Draw the graph.

Plot the point and connect them. Then, draw the axis of symmetry.