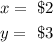Question

Let x represent the cost of an item on the top shelf and y represent the cost of an item on the bottom shelf. You can purchase 4 items from the top shelf and 2 items from the bottom shelf for $14.Equation_________You can purchase 2 items from the top shelf and 5 items from the bottom shelf for $ 19.Equation__________Solve the system of equations using elimination

Answer 1

Suppose x represents the cost of an item on the top shelf, y represents the cost of an item on the bottom shelf.

Statement 1: You can purchase 4 items from the top shelf and 2 items from the bottom shelf for $14.

Mathematically, we have;

`\begin{gathered} 4x+2y=14 \\ 2(2x+y)=14 \\ 2x+y=(14)/(2) \\ 2x+y=7\ldots\ldots..\ldots..\ldots\ldots\ldots\text{.}\mathrm{}\text{equation 1} \end{gathered}`

Statement 2: You can purchase 2 items from the top shelf and 5 items from the bottom shelf for $ 19.

Mathematically, we have;

`2x+5y=19\ldots\ldots..\ldots\ldots\ldots..\ldots\ldots\ldots\text{.equation 2}`

Then, we would solve the system of equations using elimination method.

Subtract equation 1 from equation 2, we have;

`\begin{gathered} 2x-2x+5y-y=19-7 \\ 4y=12 \\ y=(12)/(4) \\ y=3 \end{gathered}`

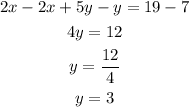
Then, we substitute the value of y in equation 1, we have;

`\begin{gathered} 2x+y=7 \\ 2x+3=7 \\ 2x=7-3 \\ 2x=4 \\ x=(4)/(2) \\ x=2 \end{gathered}`

Thus, the cost of an item on the top shelf and the bottom shelf respectively are;

`\begin{gathered} x=\text{ \$2} \\ y=\text{ \$3} \end{gathered}`