Question

The graph of a periodic function f is shown below.What is the period of f?What is the minimum value of f(θ)?What is the maximum value of f(θ)?What is the midline for f?y=What is the amplitude of f?Write a function formula for f. (Enter "theta" for θ.)f(θ)=

Answer 1

The equation the graph below represent is

y = 3 cos (2x) + 1

The period of the function is 3.14

minimum value = -2

maximum value = 4

midline = 1

amplitude = 3

How to the equation graphed

The general equation is of the form

y = A cos (Bx + C) + D

A: amplitude of the graph

= 4 - (-2) / 2

= 6 / 2

= 3

A = 3

B: = number of revolution in 2π. From the graph, there are 2 revolutions in 2π.

B = 2

Period = 2π/2

Period = π = 3.14

C: phase shift = 0

D: Vertical shift = (The maximum y-value + minimum y-value)/2

= (4 + (-2)) / 2

= 2/2

= 1

plugging in the values

y = 3 cos (2x + 0) + 1

y = 3 cos (2x) + 1

Answer 2

ANSWERS:

• Maximum value: ,4

,

• Minimum value: ,-2

,

• Midline: ,y = 1

,

• Amplitude: ,3

,

• Period: ,3.14

,

• Function: ,f(θ) = 3*cos(2*θ) + 1

Step-by-step explanation:

The maximum and minimum values of the function are the values of y for which the function has a peak. The highest peak is the maximum and the lowest peak is the minimum.

In pink we have the maximum: 4. In orange we have the minimum: -2.

To find the midline we have to know first the distance between the maximum and the minimum values:

`d=4-(-2)=4+2=6`

The midline is half the distance between the minimum and the maximum:

`\text{midline}=(d)/(2)+4=(d)/(2)+(-2)=1`

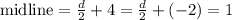
In the image above it's marked in green.

The amplitude is the distance between the maximum or minimum to the midline. In other words it's half the distance between the maximum and minimum: 3

The period is the distance between two maximums or two minimums, because that's the part that repeats after. In the graph I've marked two maximums in red: one is at θ = 0 and the other one is at θ = 3.14. Therefore the period is 3.14

Finally, the function is a cosine - because it starts at the higher value while the sine starts at zero - with an amplitude of 3, shifted 1 unit up (because the midline is 1 and not 0) and since the period is 3.14 it is also dilated horizontally by a factor of 2: f(θ) = 3cos(2θ) + 1