Question

Please determine the equation of the circle:Eqaurion should look the the example below!

Answer 1

Given a graph of the circle.

We have to determine the equation of the circle.

It is clear from the figure that the circle passes through (7, 2) and (7, -4).

The midpoint of the line joining these points is the center of the circle is:

`((7+7)/(2),(2-4)/(2))=(7,-1)`

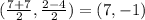
Thus, the center of the circle is (7, -1).

Now, the distance from the center to (7,2) is the radius of the circle:

`\begin{gathered} \sqrt[]{(7-7)^2+\mleft(-1-2\mright)^2}=\sqrt[]{0+(-3)^2} \\ =\sqrt[]{9} \\ =3 \end{gathered}`

Thus, the radius of the circle is 3 units.

We know that the equation of the circle is given by:

`(x-h)^2+(y-k)^2=r^2`

Here, (h, k) is the radius of the circle.

So, the equation of the given circle is:

`\begin{gathered} (x-7)^2+(y-(-1))^2=3^2 \\ (x-7)^2+(y+1)^2=9 \end{gathered}`

Thus, the answer is (x -7)^2 + (y + 1)^2 = 9.