ANSWER
0.328175
Step-by-step explanation
The two events mentioned are:
• A: exactly 1 child is a girl
,
• B: exactly 2 children are girls
These events are not-overlapping because if exactly 1 of the 6 children is a girl, then there cannot be exactly two girls at the same time - and vice versa.
The probability that the family has exactly one girl or exactly two girls is,

If there are 6 children in the family, the probability of randomly meeting a 6-child family with exactly 1 girl follows a binomial distribution, where the probability that a child is a girl is 0.5,
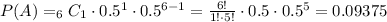
While the probability that the family has exactly 2 are girls is,

So, the probability that the family has exactly 1 girl or exactly 2 girls is,
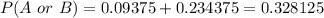
Hence, the probability of meeting a 6-child family with either exactly one or exactly two girls is 0.328175.