SOLUTION
To solve the problem, we heed to calculate the mean of the data set in the two situations i,e with the data set and without the data set.
An outlier is an extreme value in a data set that is either much larger or much smaller than all the other values
Using the formula for mean we have
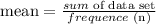
The data set is giving as
hence
The mean with the outiers will be
![\operatorname{mean}=\text{ }\frac{\text{20+35+40+45+45+50+75}}{7}=(310)/(7)=44.29]()
Mean = 44.29
In the data set, we need to calculate the outliers, using the formula

Then for the upper quartile Q3, we have
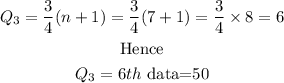
Then the inter-quartile range IQR is
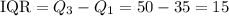
Then applying the rule for the outliers, we have
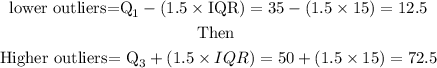
Hence
The outliers will be an of the dataset that is greater than the higher outliers or lower outliers,
Hence
The outliers is
Hence removing 75 from the data set we will have
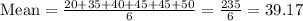
Mean= 39. 17
Hence
Removing the outlier in the data set reduces the mean
Answer= The mean will decrease (Option B)