Question

Question 10 of 10 What is the recursive formula for the geometric sequence with this explicit formula? •(-3) la = 9 O A. OA, an ar-1 0 la = -9 = O B. an = an-1 . im 3 OC. 3 a = an-1 • (-9) (2, - - 1/2 a 3

Answer 1

Given the explicit formula for the Geometric Sequence:

`a_n=9\cdot(-(1)/(3))^((n-1))`

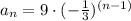
Where the nth term is:

`a_n`

Then, you need to remember that, by definition, the Recursive Formula for a Geometric Sequence has this form:

`a_n=a_(n-1)\cdot r`

Where "r" is the common ratio.

In this case, having the explicit formula with the form:

`a_n=a_1\cdot r^((n-1))`

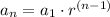
You can identify that:

`r=-(1)/(3)`
`a_1=9`

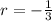
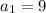
Therefore, you can set up the following recursive formula:

`a_n=a_(n-1)(-(1)/(3))`

Hence, you get:

`\begin{cases}a_1=9_{} \\ \\ a_n=a_(n-1)(-(1)/(3))\end{cases}`

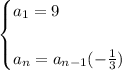
Therefore, the answer is: Option A.