ANSWER
F' (-5, 3)
E' (6, 3)
D' (1, -4)
Step-by-step explanation
We are given the cordinates of the triangle as:
F(-10, 6), E(12, 6) and D(2, -8)
The dilation factor is 1/2.
To find the new cordinates, we simply multiply the cordinates of the triangle given by 1/2.
That is:
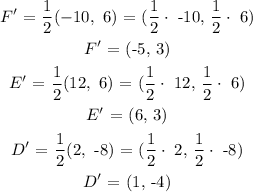
So, the cordinates of the image are:
F' (-5, 3)
E' (6, 3)
D' (1, -4)