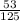Question

A bag contains 36 red blocks, 49 green blocks, 23 yellow blocks, and 17 purples blocks. You pick one block from the bag at random. Find the indicated theoretical probability P(red or purple)

Answer 1

Given that

`\begin{gathered} number\text{ of red blocks}\Rightarrow36 \\ number\text{ of green blocks}\Rightarrow49 \\ number\text{ of yellow blocks}\Rightarrow23 \\ number\text{ of purple blocks}\Rightarrow17 \\ Total\text{ numbr of blocks}\Rightarrow125 \end{gathered}`

The probability of an event is expressed as

`Pr(event)=\frac{number\text{ of desired outcome}}{total\text{ nu,ber of possible outcome}}`

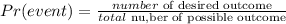
In this case, the total number of possible outcome equals 125.

Step 1: Evaluate the probability of picking a red block.

Thus,

`\begin{gathered} Pr(red)=\frac{number\text{ of red blocks}}{total\text{ numbr of blocks}} \\ =(36)/(125) \end{gathered}`

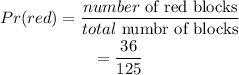
Step 2: Evaluate the probability of picking a purple block.

Thus,

`\begin{gathered} Pr(purple)=\frac{number\text{ of purple blocks}}{total\text{ number of blocks}} \\ =(17)/(125) \end{gathered}`

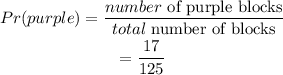
Step 3: Evaluate the probability of picking a red or purple block.

The probability of picking a red or purple block is expressed as

`Pr(red\text{ or Purple\rparen=Pr\lparen red\rparen+Pr\lparen purple\rparen}`

Thus, we have

`\begin{gathered} Pr(red\text{ or purple\rparen=}(36)/(125)+(17)/(125) \\ \Rightarrow Pr(red\text{ or purple\rparen=}(53)/(125) \end{gathered}`

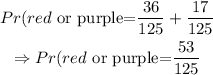
Hence, we have the theoretical probability P(red or purple) to be

`(53)/(125)`