Question

A sparkling water distributor wants to make up 300 gal of sparkling water to sell for $6.00 per gallon. She wishes to mix three grades of water selling for $10.00, $1.00, and $4.50 per gallon, respectively. She must use twice as much of the $4.50 water as the $1.00 water. How many gallons of each should she use?

Answer 1

Let's call x, y, and z the $10, $1, and $4.50 water respectively.

`x+y+z=300`

Because the total is 300 gallons.

"She must use twice as much of the $4.50 water as the $1.00 water" we express it like this

`z=2y`

We combine equations

`\begin{gathered} x+y+2y=300 \\ x+3y=300 \end{gathered}`

We know that we have to mix all three grades of water for $6.

`10x+y+4.5z=6(300)`

We combine the second equation with the last one

`\begin{gathered} 10x+y+4.5(2y)=1800 \\ 10x+y+9y=1800 \\ 10x+10y=1800 \\ 10(x+y)=1800 \\ x+y=(1800)/(10) \\ x+y=180 \end{gathered}`

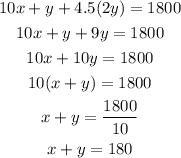
Now, we combine the last question with x+3y = 300 to make a system

`\begin{cases}x+3y=300 \\ x+y=180\end{cases}`

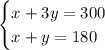
We multiply the second equation by -1, then we combine the equations to solve for y

`\begin{gathered} \begin{cases}x+3y=300 \\ -x-y=-180\end{cases}\rightarrow x-x+3y-y=300-180 \\ 2y=120 \\ y=(120)/(2) \\ y=60 \end{gathered}`

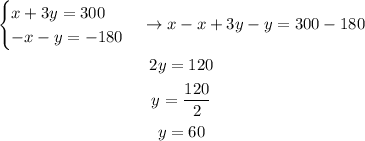
This means she should use 60 gallons of the $1 water.

Then,

`\begin{gathered} x+y=180 \\ x+60=180 \\ x=180-60 \\ x=120 \end{gathered}`

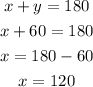
She should use 120 gallons of the $10 water.

At last,

`\begin{gathered} x+y+z=300 \\ 120+60+z=300 \\ z=300-180 \\ z=120 \end{gathered}`

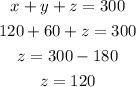
She should use 120 gallons of $4.50 water.