There are 7 letters in a box, shown as TRACKED. We have to pick up 5 letters in the order such that the outcome is TRACE.
a)
Let each letter is picked with replacement.
So, the probability of picking up letter T first is,

We replaced the picked up letter T. So, the number of letters 7 in the box remains the same. Now, the probability of picking up letter R is,
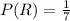
Similarly, the probability of picking up letters A,C and E respectively with replacement is,
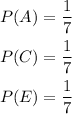
Hence, the probability of the outcome TRACE in that order if 5 letters are drawn one by one with replacement is,
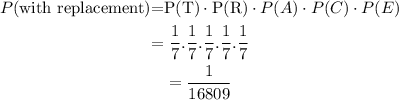
So, the probability of the of the outcome TRACE in that order if 5 letters are drawn one by one with replacement is 1/16809.
b)
Let each letter in TRACE is picked in order without replacement.
So, the probability of picking up letter T first is,

Now, there are only 6 letters remaining in the box. So, the probability of picking up letters R without replacement is,
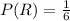
Similarly, the probability of picking up letters A,C and E respectively without replacement is,
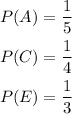
Now, the probability of the outcome TRACE in that order if 5 letters are drawn one by one without replacement is,

Therefore, the probability of the outcome TRACE in that order if 5 letters are drawn one by one without replacement is 1/2520.