In order to calculate the best airfare for 1300 miles, we need to fit a line to represent these points using linear regression.
The line can be calculated using the following equations:
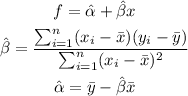
Calculating the average value of x and y, we have:
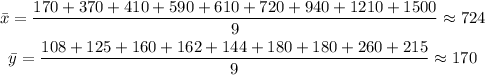
Now, calculating the value of Beta, we have:
![\begin{gathered} \hat{\beta}=((-554)(62)+(-354)(45)+(-314)(10)+(-134)(8)+(-114)(26)+(-4)(-10)+(216)(-10)+(486)(90)+(776)(45))/((-554)^2+(-354)^2+(-314)^2+(-134)^2+(-114)^2+(-4)^2+(216)^2+(486)^2+(776)^2) \\ \hat{\beta}=(19086)/(1446824)=0.01319 \end{gathered}]()
Calculating Alpha, we have:
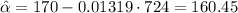
So our function is:
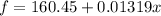
Using the value of x = 1300, we have:
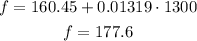
So the value that best represent the cost is $180, therefore the answer is the first option.