Question

Graph a right triangle with the two points forming the hypotenuse. Using the sides,find the distance between the two points in simplest radical form.(4, -2) and (-1,-6)Click twice to droulim01:

Answer 1

We are given the points that form the hypothenuse side as:

(4,-2) and (-1, -6)

To find the distance (d) between the two points, we use the formula below:

`d\text{ = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Where (x1,y1) and (x2, y2) are the points

By substituting the given points (4, -2) and (-1, -6), we have:

`\begin{gathered} d\text{ = }\sqrt[]{(-1-4)^2+(-6-(-2))^2} \\ d\text{ = }\sqrt[]{25\text{ +16}} \\ d\text{ = }\sqrt[]{41} \end{gathered}`

To find the length of leg 1, we should identify the points that form leg 1, which are:

(-1, -2) and (-1, -6)

Using the formula above, the length (l) of leg 1 is:

`\begin{gathered} l\text{ = }\sqrt[]{(-1-(-1))^2+(-6-(-2))^2} \\ =\text{ }\sqrt[]{0+16} \\ =\text{ 4} \end{gathered}`

To find the length of leg 2, we can apply the Pythagoras theorem since the triangle is right-angled

`\text{Hypothenus}^2=Opposite^2+Adjacent^2`

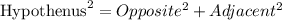
In this case, the length of leg 2 is adjacent. let us label it as x.

`\begin{gathered} (\sqrt[]{41)}^2=4^2+x^2 \\ 41=16+x^2 \\ x\text{ = }\sqrt[]{25} \\ x\text{ = 5} \end{gathered}`

Answers: leg 1 = 4 units, leg 2 = 5 units, hypothenuse side = sqrt(41)