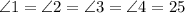A rhombus has:
- 2 opposite angles which are congruent and
- the four angles add up 360 degrees.
The first statement means that
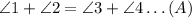
The second statement means that
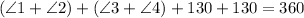
By rewritten this equation, we have
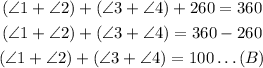
By substituying equation A into B, we have
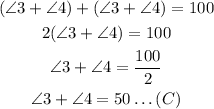
A particular property of rhombus is that
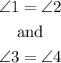
By substituying the last equality into equation C, we have
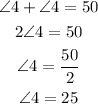
Therefore, we have
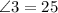
And finally, we can see that, necesarilly,