Question

Karl is building a rectangular garden bed. The length is 6 feet. She has 20 feet of boards to make the sides. Write and solve an inequality to find the possible width of her garden bed.

Answer 1

The width of the garden bed must be less than or equal to 4 feet.

`w\leq4`

Step-by-step explanation:

Given that;

She has 20 feet of boards to make the sides.

The perimeter of the garden bed must not be more than 20 feet

`\begin{gathered} P=2l+2w\leq20 \\ 2l+2w\leq20 \end{gathered}`

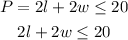
Given;

The length is 6 feet;

`l=6`

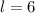
To get the inequality for the width w, let us substitute the value of the length into the inequality above and simplify;

`\begin{gathered} 2l+2w\leq20 \\ 2(6)+2w\leq20 \\ 12+2w\leq20 \\ 2w\leq20-12 \\ 2w\leq8 \\ (2w)/(2)\leq(8)/(2) \\ w\leq4 \end{gathered}`

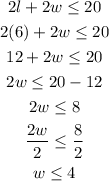
Therefore, the width of the garden bed must be less than or equal to 4 feet.

`w\leq4`