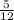Given that a coin is tossed and a die is rolled.
Let's find the probability of getting a head and a number greater than 1.
To find the probability of getting a head and a number greater than 1, apply the formula:
P(head and 1) = P(head) x P(greater than 1)
Where:
Number of heads in a coin = 1
A coin contains a head and a tail. ==> 2 possible outcomes
Numbers greater than one in a die = 2, 3, 4, 5, 6, ==> 5 numbers.
A dies contains 6 numbers ==> 6 possible outcomes
Therefore, we have:

Thus, finding the probability, we now have:
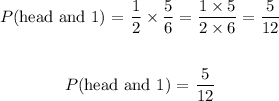
Therefore, the probability of getting a head and a number greater than 1 is:
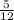
ANSWER: