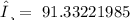You have to use the following formula to calculate the angle between TWO vectors:
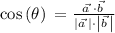
In this case the vector u will be the vector a, and the vector v will be the vector b
To replace the formula, we have to know the dot product:
In this case a * b
Multiply each i and each j
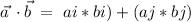
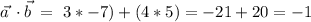
Now
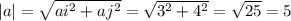
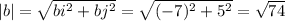
Now replace in
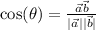
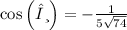
Clear Cos with ArcCos
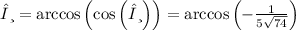
ANS: