we are given the measures of three angles of a triangle in the form of polynomials. Let's remember that the sum of the angles of a triangles is always 180. Therefore, the sum of the three given polynomials must be 180, from there we can solve for "x", like this:
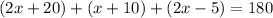
We will add like terms, we get:
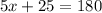
subtracting 25 on both sides of the equation

Now we divide by 5 on both sides of the equation
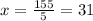
Now that we have the value of "x" we can replace it in the polynomials and find the largest of them, like this
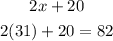
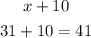
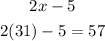
Therefore, the largest angle is 82