Question

Please help me with this problem! I keep getting it wrong and im not sure what to do.

Answer 1

Okay, here we have this:

Considering the provided equation, we are going to find the solution in the interval, so we obtain the following:

`\begin{gathered} \sin \mleft(2\theta\mright)=(√(3))/(2),\: 0\le\: \theta<\: 2\pi \\ 2\theta=(\pi)/(3)+2\pi n,\: 2\theta=(2\pi)/(3)+2\pi n \\ \theta=(\pi)/(6)+\pi n,\: \theta=(\pi)/(3)+\pi n \end{gathered}`

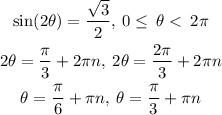
Now we analyze which are the solutions that are within the range, then finally we have:

`\theta=(\pi)/(6),\: \theta=(\pi)/(3),\: \theta=(7\pi)/(6),\: \theta=(4\pi)/(3)`

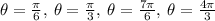
The above values are the solution set of the equation.