Givens.
• The angular speed is 3 revolutions per minute.
,
• The linear speed is 3.8 ft/sec.
Use the formula that includes linear speed, angular speed, and radius.
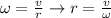
But, we need to transform the angular speed from revolutions per minute to radians per second.

Once you have the right units, find the radius.
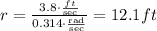
Therefore, the horse is 12.1 feet from the center.