GIVEN:
We are told that a repairman earns $12 for each bathroom sink he repairs and $59 for each tub he repairs.
Last week he repaired a total of 23 items and the total pay for the week was $652.
Required;
We are required to determine how many of each type of item did he repair.
Step-by-step solution;
We shall begin by assigning variables to the items and these will be;
Let fiberglass bathroom sink be x.
Let fiberglass tub be y.
if he repaired a total of 23 items, then we can set up the following equation;
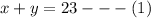
For each bathroom sink repaired he earns $12. That means if he repairs 2, then he would earn $12 times 2, and so on. This means if he repairs x number of fiberglass bathroom sink he would earn 12x.
The same applies to his fiberglass tub earnings. he would earn 59y if he repairs y number of tubs.
He makes a total of $652 for the week. That means for all his repairs, we can set up the following equation;
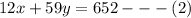
We can now solve the system of equations by using the substitution method;
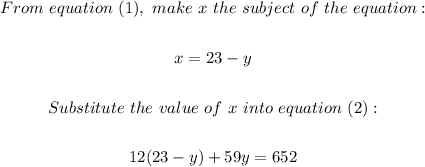
We can now simplify and we'll have;
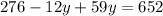
We can now collect like terms;

Note that the number 276 has crossed the equality sign and therefore has switched signs (from positive to negative).

We can now substitute the value of y into equation (1);

Therefore, we have
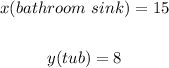
ANSWER:
The items he repaired during the week were;
15 fiberglass bathroom sink
8 fiberglass tub