Question

1. m = 3/2, b = -42.m = -3/2, b = 4determine how many solutions this can have.One ZeroInfinite

Answer 1

First let's write each equation using the slope-intercept form:

`y=mx+b`

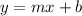
So we have the following system:

`\begin{cases}y=(3)/(2)x-4 \\ y=-(3)/(2)x+4\end{cases}`

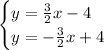
In order to solve this system, let's add both equation, this way we can find the value of y and then the value of x:

`\begin{gathered} y+y=(3)/(2)x-4+(-(3)/(2)x)+4 \\ 2y=0 \\ y=0 \\ \\ 0=(3)/(2)x-4 \\ (3)/(2)x=4 \\ 3x=8 \\ x=(8)/(3) \end{gathered}`

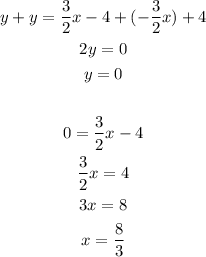
So the solution to this system is (8/3, 0), therefore the system has one solution.