$41958 must be paid back
Step-by-step explanation:
AMount borrowed = P = $27000
time = t= 7 years
n = compounded annually
n = 1
rate = 6.5% = 0.065
Amount to be paid back at the end of the period = FV
We will be apply the compound interest formula:
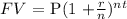
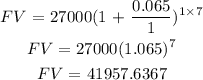
To the nearest dollar, $41958 must be paid back