Question

from a sample with n=8, the mean number of televisions per household is 2 with a standard deviation of 1 television. using chebychevs theorem, determine at least how many households have between 0 and 4 televisions

Answer 1

n=8

Mean number of televesions per household= 4

Standard deviation= 1

Find the number of households have between 0 and 4 television

As a first step we are going to check the within numbers:

So, now, we can find the value of k:

`\begin{gathered} k=\frac{\text{within number}}{\text{standard deviation}} \\ k=(4)/(1)=4 \end{gathered}`

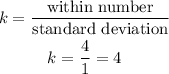
Now, using the chebychev's theorem:

`1-(\frac{1^{}}{k})^2\text{ }`
`1-(1)/(16)=(15)/(16)`

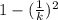
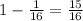
Then, the number of the house holds would be:

`(15)/(16)\cdot8=(15)/(2)=7.5`

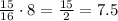
There are at least 7.5 households that have between 0 and 4 televisions