Question

Which of the following equations describes the nth term for the sequence two thirds comma one third comma one sixth comma one twelfth and continues question mark

Answer 1

The sequence given represents a Geometric Sequence.

The general formula for a GP is given to be:

`a_n=a_1(r)^(n-1)`

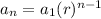
where

`\begin{gathered} a_1=\text{ first term} \\ r=\text{ common ratio} \end{gathered}`

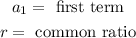
From the sequence in the question, the first term is:

`a_1=(2)/(3)`

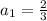
The common ratio can be calculated by dividing consecutive terms, that is s term divided by the preceding term.

Hence, the common ratio is given to be:

`\begin{gathered} r=(1)/(3)/(2)/(3) \\ r=(1)/(3)*(3)/(2) \\ r=(1)/(2) \end{gathered}`

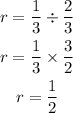
Therefore, the nth term for the sequence is:

`a_n=(2)/(3)((1)/(2))^(n-1)`

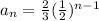
The correct option is the FIRST OPTION.