Question

Please make sure you answer both parts of the question. Remember to properly format your function.George bought a big yellow hat on a credit card for $12.47. The credit card had an annual percentage rate (APR) or 24.8%.1: Write an exponential function that can be used to model this function.2: If George made no payments on the hat for 12 years (assuming no additional fees), how much money would he owe for the purchase?

Answer 1

Part 1

Lets say that C represents the cost of the hat as we buy it using the credit card. Let Co be the initial cost of the hat and let i be the interest rate. Also if n is the number of periods of time the cost of the hat changes, then our function can be:

`C=C_o(1+i)^n`

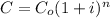
where:

Co = initial cost = $12.47

i = interest rate = 24.8% = 24.8 / 100 = 0.248

n = number of periods of time

Then:

`C=C(n)=12.47*(1+0.248)^n`

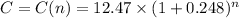
So the final answer for part 1 is:

`C(n)=12.47*(1.248)^n`

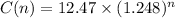
Part 2

To solve this we must take n = 12 and plug in the function above. We get:

`\begin{gathered} C(12)=12.47*(1.248)^(12) \\ C(12)=12.47*(14.275) \\ C(12)=178.01 \end{gathered}`

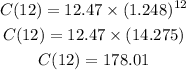
So the final answer for part 2 is:

`C(12)=178.01`

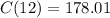
George would owe $178.01 for the purchase.