Question

Help me answer this question please ( I got 2 and 3 and they are both wrong)

Answer 1

Step-by-step explanation:

The critical points are the points where the derivative of a function is zero or is not defined.

In this problem we have a function that's a polynomial and so, it's derivative is also a polynomial. Therefore, it has no value where it's not defined. However, there will be points where it's zero.

Let's find the derivarive first:

`(dg(x))/(dx)=g^(\prime)(x)=15x^4-15x^2`

We can rewrite it as:

`g^(\prime)(x)=15x^2(x^2-1)`

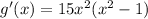
So the zeros are now very easy to find. We can see that if x = 0, since we have x² multiplying, the whole function is zero. This is one critical point.

Then the function is also zero when (x²-1)=0:

`\begin{gathered} x^2-1=0 \\ x^2=1 \\ x=\pm\sqrt[]{1} \\ x=\pm1 \end{gathered}`

The other two critical points are 1 and -1.

Answer:

There are 3 critical points within the domain: -1, 0, 1