Given:
Based on a recent study, the pH level of the arterial cord (one vessel in the umbilical cord) is normally distributed.
The mean = μ = 7.21
The standard deviation = σ = 0.15
For the required, we will use the following formula to use the z-score:
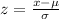
==================================================================
Find the percentage of preterm infants who have the following arterial cord pH levels.
a. pH levels between 7.00 and 7.50.
So, we will find the value of z-score when x = 7 and when x = 7.5
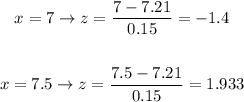
So, we will find the probability of P( -1.4 < z < 1.933 ) from the z-tables
![P(-1.4The answer as a percentage = <strong>89.26%</strong><p>==================================================================</p><p> Find the percentage of preterm infants who have the following arterial cord pH levels. b. pH levels over 7.29.</p><p></p><p>So, we will find the value of the z-score when x = 7.29</p>[tex]x=7.29\to z=(7.29-7.21)/(0.15)=0.533](https://img.qammunity.org/2023/formulas/mathematics/college/5dcozwcp9pkkfg60x0xgrn6rf5s4s8ufnl.png)
So, we will find the probability of P ( z > 0.533 )from the z-tables
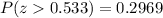
So, the answer as a percentage = 29.69%
=================================================================